矢量运算与标准化 normalized

矢量运算是数学中一个较为基础的知识，在 Unity 中有较多应用。

1.矢量加减

矢量加减多用于 **相同类型 **的矢量，所产生的总体混合效果。

1.1 矢量减法

例如，从 A 点向 B 点移动时，需要知道从 B 指向 A 的方向；

在矢量运算中，可以用减法直接获取表示此方向的新矢量，即：

//从B指向A的方向计算，即A的坐标减去B的坐标
Vector3 x = A.transform.position - B.transform.position;

用二维矢量大致模拟一下，可示意如下：

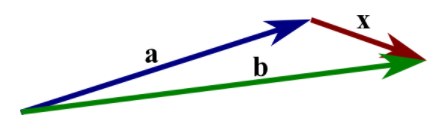
以上。

1.2 矢量加法

向量的加法满足平行四边形法则和三角形法则。

具体地，两个向量a和b相加，得到的是另一个向量。这个新向量可以表示为a和b的起点重合后，以它们为邻边构成的平行四边形的一条对角线，或者表示为将a的终点和b的起点重合后，从a的起点指向b的终点的向量；

//向上移动若干距离
Vector3 a = Vector3.up * moveSpeedU * Time.deltaTime;
//向前移动若干距离
Vector3 b = Vector3.forward * moveSpeedF * Time.deltaTime;
//最终移动的位置
transfrom.Translate(a + b);

用二维矢量大致模拟一下，可示意如下：

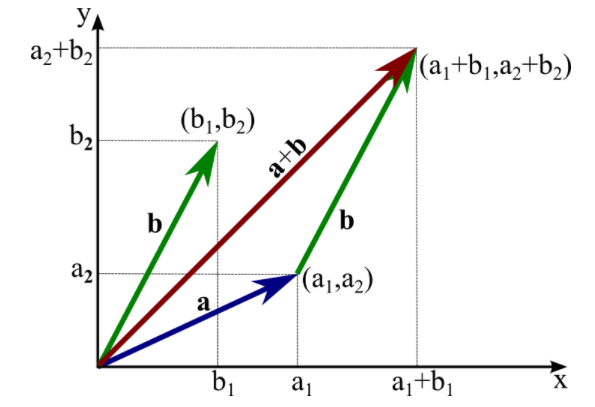
实际上 Unity 中的 transform.Translate() 方法就是在不断的进行基于位置矢量的加法操作；

2.矢量乘法

矢量乘法通常用于计算 不同类型 的矢量、或者矢量与标量之间产生的综合叠加效果；

2.1标量乘法

获得一个方向不变（标量为负时方向相反），长度按标量倍数计算的新矢量；

例如，根据方向（矢量）、速度（标量）和时间（标量），计算实际移动距离：

Vector3 moveDistance = Vector3.forward * moveSpeed * Time.deltaTime;

以上。

2.2矢量点积

暂不赘述。可参考 尾注 信息；

2.矢量标准化

使用以下函数，可将矢量标准化：

Vector3 curPos = new Vector3 (12,0,2);
//保留当前矢量，将标准化后的结果赋值给一个新矢量
Vector3 newPos = curPos.normalized;
//将当前矢量标准化
curPos.normailize;

所谓的标准化，即：

令矢量的方向保持不变，但其长度为 1.0。

实际应用时，可以用此方法获取纯粹的方向性数据，而不受距离参数的影响；

3.尾注

关于矢量运算，可以参考的资料有很多；

以下是一些初步内容：

• vectors @ mathsisfun ;
• 向量 @ 维基百科 ；

以上。